Divergence free magnetic field

This example demonstrates the resulting angular profile of an SECS pole placed at the north pole. Figure 2 from Amm and Viljanen 1999.

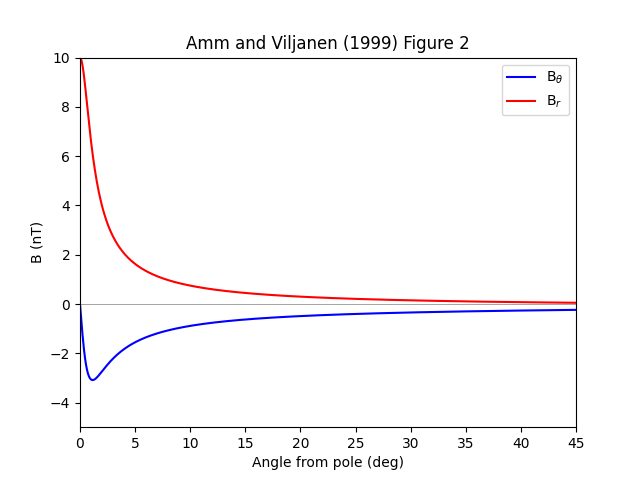
import matplotlib.pyplot as plt
import numpy as np

from pysecs import SECS


# Radius of Earth
R_E = 6378e3

# Pole of the current system at the North Pole
sec_loc = np.array([90.0, 0.0, R_E + 100e3])

# Set up the system with a single SEC
system_df = SECS(sec_df_loc=sec_loc)

# Fit unit currents since we aren't fitting to any data
system_df.fit_unit_currents()

# Scale the system corresponding to Figure 2 of
# Amm and Viljannen (1999) doi:10.1186/BF03352247
# 10 kA
total_current = 10000
system_df.sec_amps *= total_current

# Set up the prediction grid
N = 1000
pred_loc = np.zeros(shape=(N, 3))
angles = np.linspace(0, 45, N)

pred_loc[:, 0] = 90 - angles
pred_loc[:, 2] = R_E

B_pred = system_df.predict(pred_loc=pred_loc)

# B_theta == -Bx == -B_pred[:,0]
# Convert to nT (1e9)
B_theta = -B_pred[:, 0] * 1e9
# B_r == -Bz = -B_pred[:,2]
B_r = -B_pred[:, 2] * 1e9

fig, ax = plt.subplots()

ax.plot(angles, B_theta, c="b", label=r"B$_{\theta}$")
ax.plot(angles, B_r, c="r", label=r"B$_r$")
ax.legend(loc="upper right")
ax.set_xlim(angles[0], angles[-1])
ax.set_ylim(-5, 10)
ax.set_xlabel("Angle from pole (deg)")
ax.set_ylabel("B (nT)")
ax.axhline(0.0, c="k", alpha=0.5, linewidth=0.5)
ax.set_title("Amm and Viljanen (1999) Figure 2")

plt.show()